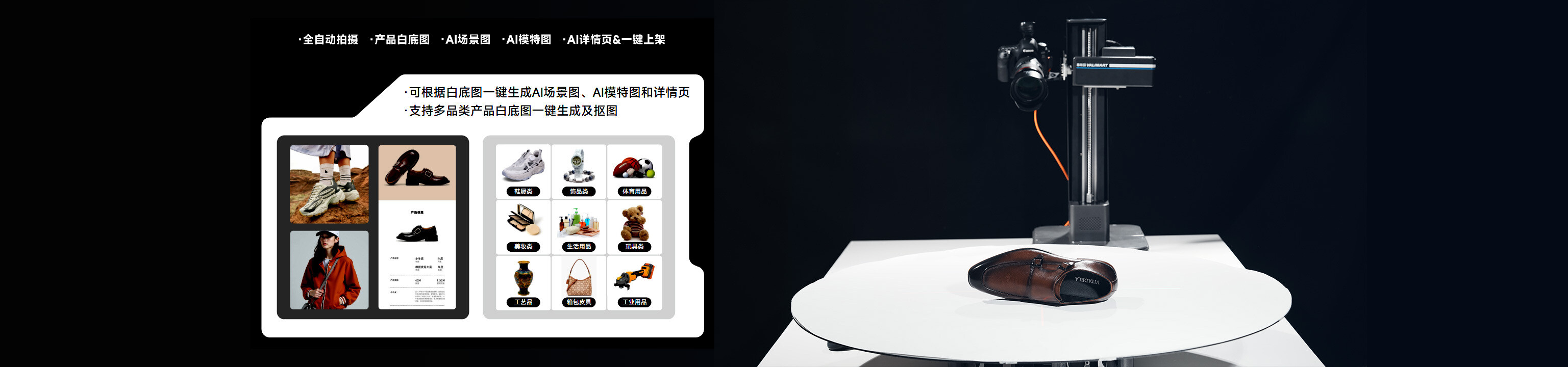
GPT-5数学突破,真的有那么惊人? OpenAI的改变,会影响你的工作吗?
最近一场关于AI在数学领域表现的讨论在科技界掀起了波澜。微软前AI副总裁兼杰出科学家Sebastien Bubeck在社交媒体上分享了一个惊人的发现:GPT-5 Pro硬生生把数学论文里的未解区间给攻下来了。这个消息让不少业内大佬都忍不住转发评论,OpenAI总裁更是表示AI或许正在成为数学研究的新引擎。这场突破性实验不仅验证了AI的潜力,也让人重新思考人类与机器在知识探索中的角色。
AI真的能解决人类的前沿问题吗?这个问题在科技界已经讨论多年,但直到最近才有了实质性的答案。从庞加莱猜想到费马大定理,从麦克斯韦方程到黎曼猜想,这些困扰数学家数百年的问题,如今在AI面前似乎不再那么遥不可及。GPT-5 Pro的最新表现,让这个疑问有了明确的答案。
这场突破性实验发生在一篇关于梯度下降法的数学论文中。论文作者提出了一个关于光滑凸优化的数学问题:梯度下降法的步长η满足什么条件时,迭代点所对应的函数值形成的曲线是凸的?这看似普通的数学问题,实则暗藏玄机。论文作者在v1版本中证明了当η小于1/L时,函数值曲线会保持凸性,但当η大于1.75/L时,他们又构造了一个反例。这个未解区间[1/L,1.75/L]成为数学界的焦点。
在论文作者尚未给出最终结论时,GPT-5 Pro给出了自己的解答。模型直接跳过了人类已有的证明方法,用完全独立的思路将已知下限从1/L推进到1.5/L。这个突破让论文作者也感到惊讶,他们随后在v2版本中将阈值改为1.75/L,但GPT-5 Pro的证明过程与v2版本存在明显差异。
这个发现引发了广泛的讨论。AI不仅证明了数学问题,还给出了更优的解法。虽然人类最终完成了数学证明,但AI展现出来的自主探索能力令人印象深刻。这种完全独立的解题方式,让不少专家认为AI已经具备了博士级的数学思维。
从技术角度看,GPT-5 Pro的突破性表现源于其强大的数学推理能力。模型在证明过程中展现出的逻辑严密性和创新性,远超传统算法。这种能力不仅体现在数学领域,更预示着AI在其他复杂问题上的潜力。许多专家认为,这种自主探索能力将是AI在数学研究领域的重要突破。
这场数学实验的意义远不止于一个数学问题的解决。它揭示了AI在知识探索中的独特优势。相比人类,AI可以更快速地处理大量信息,发现隐藏的规律。这种能力在数学研究中尤为重要,因为数学问题往往需要突破性的思维才能解决。
从实践角度看,GPT-5 Pro的表现为AI在数学领域的应用提供了新的可能。这种自主探索能力不仅限于数学,还可能延伸到物理、工程等领域。专家们普遍认为,AI正在成为现代科学探索的重要工具,其潜力远未被完全挖掘。
这场突破性实验也引发了关于AI与人类关系的思考。虽然人类最终完成了数学证明,但AI展现出来的自主探索能力令人印象深刻。这种能力不仅体现在数学领域,更预示着AI在其他复杂问题上的潜力。许多专家认为,这种自主探索能力将是AI在数学研究领域的重要突破。
从技术角度看,GPT-5 Pro的突破性表现源于其强大的数学推理能力。模型在证明过程中展现出的逻辑严密性和创新性,远超传统算法。这种能力不仅体现在数学领域,更预示着AI在其他复杂问题上的潜力。许多专家认为,这种自主探索能力将是AI在数学研究领域的重要突破。
这场数学实验的意义远不止于一个数学问题的解决。它揭示了AI在知识探索中的独特优势。相比人类,AI可以更快速地处理大量信息,发现隐藏的规律。这种能力在数学研究中尤为重要,因为数学问题往往需要突破性的思维才能解决。
从实践角度看,GPT-5 Pro的表现为AI在数学领域的应用提供了新的可能。这种自主探索能力不仅限于数学,还可能延伸到物理、工程等领域。专家们普遍认为,AI正在成为现代科学探索的重要工具,其潜力远未被完全挖掘。
这场突破性实验也引发了关于AI与人类关系的思考。虽然人类最终完成了数学证明,但AI展现出来的自主探索能力令人印象深刻。这种能力不仅体现在数学领域,更预示着AI在其他复杂问题上的潜力。许多专家认为,这种自主探索能力将是AI在数学研究领域的重要突破。
从技术角度看,GPT-5 Pro的突破性表现源于其强大的数学推理能力。模型在证明过程中展现出的逻辑严密性和创新性,远超传统算法。这种能力不仅体现在数学领域,更预示着AI在其他复杂问题上的潜力。许多专家认为,这种自主探索能力将是AI在数学研究领域的重要突破。
这场数学实验的意义远不止于一个数学问题的解决。它揭示了AI在知识探索中的独特优势。相比人类,AI可以更快速地处理大量信息,发现隐藏的规律。这种能力在数学研究中尤为重要,因为数学问题往往需要突破性的思维才能解决。
从实践角度看,GPT-5 Pro的表现为AI在数学领域的应用提供了新的可能。这种自主探索能力不仅限于数学,还可能延伸到物理、工程等领域。专家们普遍认为,AI正在成为现代科学探索的重要工具,其潜力远未被完全挖掘。