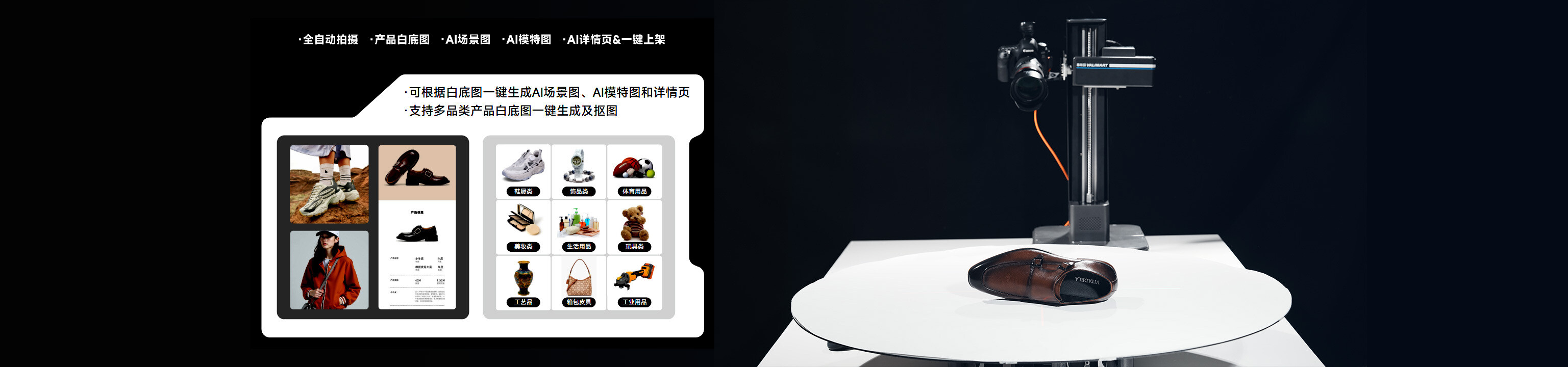
强化学习的瓶颈,到底藏在哪里?AI服装工具,能突破它吗?
### 神经强化学习几何结构:连续状态与动作空间中的低维流形
---
#### **一、理论基础:智能体可达状态的低维几何结构**
1. **核心主张**
强化学习智能体在连续状态和动作空间中,其可达状态集收敛于一个**低维流形**,其维度由动作空间维度 $ d_a $ 决定,上界为 $ d_a $。
2. **关键推导步骤**
- **策略线性化**:将神经网络策略参数化为宽两层前馈网络,并线性化处理,将其视为一个矢量场(如公式(10))。
- **轨迹展开**:利用**李级数**对智能体状态轨迹进行展开,保留到二阶项,分析其动态变化(公式(7))。
- **基向量分析**:证明一阶项(速度)和二阶项(加速度)均可由一组数量约为 $ d_a $ 的基向量线性表示。
- **维度约束**:所有局部可达状态均位于一个维度为 $ d_a $ 的空间内,拼接形成**低维流形**(定理1)。
3. **数学原理**
- **李级数展开**:
$$
\text{新状态} \approx \text{当前状态} + \Delta t \cdot \text{瞬时速度} + \frac{1}{2} \Delta t^2 \cdot \text{加速度} + \dots
$$
其中,瞬时速度由策略决定,自由度受限于动作空间维度 $ d_a $;加速度项的自由度同样由 $ d_a $ 和学习动态决定。
---
#### **二、实验验证与应用**
1. **实验一:线性化近似有效性**
- **目标**:验证线性化宽网络对真实神经网络的合理性。
- **方法**:在Cheetah环境中比较标准两层网络与线性化版本的奖励差异。
- **结论**:随着网络宽度增加,奖励差值趋近于0,证明线性化假设成立。
2. **实验二:可达状态维度估计**
- **目标**:验证内在维度是否满足理论上界。
- **方法**:在四个MuJoCo任务中使用DDPG训练智能体,通过内在维度估计算法分析状态集。
- **结论**:估计的内在维度(蓝色曲线)显著低于状态空间维度(绿色线),且始终低于理论上界(红色线)。
3. **实验三:算法改进(稀疏SAC)**
- **目标**:利用低维几何结构改进算法性能。
- **方法**:在SAC算法中替换全连接层为稀疏化层,利用低维流形结构。
- **结论**:稀疏SAC(红色曲线)性能显著优于原始SAC(蓝色曲线),验证理论洞见的实用性。
---
#### **三、主实验设计与消融分析**
1. **主实验设计**
- **任务选择**:四个经典的MuJoCo连续控制任务(如Ant、HalfCheetah),均为连续状态和动作空间的典型场景。
- **评价指标**:内在维度估计,直接验证核心主张。
- **基线对比**:与状态空间维度和理论上界对比,凸显结论的显著性。
2. **消融实验**
- **实验一**:验证线性化宽网络假设的合理性(证明理论分析相关性)。
- **实验三**:证明利用低维结构改进算法的必要性(稀疏SAC性能提升)。
---
#### **四、深度实验:函数类别对问题复杂度的影响**
1. **实验设计**
- **环境构建**:在完全可控的线性系统中,限制策略为有界的神经网络,固定动作维度 $ d_a $,增加状态维度 $ d_s $。
- **关键发现**:尽管系统“完全可控”,但神经网络策略下可达状态的内在维度被钉在理论上界 $ d_a $ 之下,不随 $ d_s $ 增加而变化。
2. **洞见**
- **问题复杂度来源**:不仅取决于环境动力学,还由**函数类别**(如神经网络)决定。
- **理论意义**:揭示了函数表示对问题内在结构的塑造作用,为算法设计提供新视角。
---
#### **五、核心贡献与创新点**
1. **理论贡献**
- 首次系统性地将**几何结构**引入神经强化学习,证明可达状态集的低维性。
- 通过李级数和基向量分析,建立动作空间维度与状态流形维度的数学联系。
2. **应用价值**
- **算法改进**:稀疏化层设计(如稀疏SAC)显著提升性能,适用于高维连续控制任务。
- **理论指导**:为理解强化学习的内在机制提供几何视角,推动算法优化与理论深化。
3. **创新性实验**
- 在可控环境中验证理论与经典控制理论的差异,揭示函数类别对问题复杂度的决定性影响。
---
#### **六、总结**
本文通过理论分析和实验验证,揭示了神经强化学习在连续状态和动作空间中的**低维几何结构**,证明可达状态集受动作空间维度限制。这一发现不仅深化了对强化学习机制的理解,还为设计高效算法提供了新方向。未来可进一步探索不同函数类别(如Transformer、图神经网络)对问题复杂度的影响,拓展理论应用边界。